TPMS车轮自动定位算法介绍(NXP)-3
4.2移动路径与旋转周期之间的关系
旋转周期是指车轮执行完整旋转所需的时间。
这是车轮行驶距离等于其周长(周长=2π)的时间✕ 车轮半径)。以下等式适用:
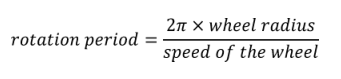
•在给定速度下,随着车轮周长的增加,车轮的旋转周期也会增加。如果车轮周长较大,则车轮需要更多时间来执行旋转。
•对于给定的车轮半径,速度越高,旋转周期越短。如果速度更高,车轮在更短的时间内执行旋转。
这两个参数会影响旋转周期的绝对值,但不会影响转弯时四个车轮旋转周期之间的相对差异。
显示速度对旋转周期的影响
•汽车以20度的转向角左转,内前轮以20度的角度转动。车轮半径为24厘米。
•第一种情况−汽车以每小时40公里的速度行驶
•第二种情况−汽车以每小时10公里的速度行驶
在第一种情况下,四个车轮的旋转周期如下:
•右前轮:125毫秒
•右后轮:130.5毫秒
•左前轮:148毫秒
•左后轮:157.5毫秒
两个右车轮之间的差值为5.5 ms。这表示右前轮周期的4.4%。
两个左车轮之间的差值为9.5 ms。这代表了左前轮周期的6.4%。
5.5 ms/9.5 ms = 57.9%
在第二种情况下,四个车轮的旋转周期如下:
•右前轮:500毫秒
•右后轮:522毫秒
•左前轮:592毫秒
•左后轮:630毫秒
两个右车轮之间的差值为22 ms。这表示右前轮周期的4.4%,与场景1中的百分比相同。
两个左轮之间的差值为38 ms。这代表了左前轮周期的6.4%,与场景1中的百分比相同。
22 ms/38 ms = 57.9%
在本例中,降低速度会增加四个旋转周期,但不会增加它们之间的相对差异。增加车轮半径也会得出相同的结论。
在算法中,车速是一个必要的考虑因素吗?是的,因为比较高数值比比较低数值更容易、更可靠,因为数据离噪声级更远。22毫秒的旋转周期(第二种情况)比5.5毫秒的旋转周期更容易看出差异,这接近于噪声造成的不精确性(第一种情况)。在本例中,区分车轮在10 km/h时比在40 km/h时更可靠。这就是为什么该算法仅在低速时使用,从大约3 km/h到30 km/h。区分大半径车轮更容易,因为增加车轮半径会增加旋转周期。如果车轮半径较小,则旋转周期较短,两者之间的差异接近噪声级。
总之,速度和车轮半径这两个参数对旋转周期的绝对值有影响,但它们不会增强旋转周期之间的相对差异。
注:来源于网络整理